Skip to content

📈 Visualizing High-Dimensional Data

(Parallel Coordinates · Deviation Chart · Andrews Curve)

1️⃣ Introduction

When data has more than three dimensions, standard 2D or 3D plots fail to reveal structure.
We use specialized projection and transformation techniques to visualize multivariate patterns:

  • Parallel Coordinate Plots (PCP) — visualize multi-attribute records as lines.

  • Deviation Charts — highlight differences from a baseline (useful for comparisons).

  • Andrews Curves — map multivariate points to continuous periodic functions.

2️⃣ Parallel Coordinate Chart (PCP)

Theory

Given \(p\) variables \(( x_1, x_2, ..., x_p )\), each record \(( i )\) is a vector
\((\mathbf{x}^{(i)} = (x^{(i)}_1, x^{(i)}_2, \dots, x^{(i)}_p))\) Each variable is drawn on a parallel axis.

Each record is plotted as a polyline connecting values across axes.

Mathematical Normalization

\((x'_{ij} = \dfrac{x_{ij} - \min(x_j)}{\max(x_j) - \min(x_j)})\)

Manual Example

Original data and normalized values (min=10, max=30 for all three variables):

Observation X1 X2 X3
A 10 20 30
B 20 10 40
C 30 30 20

Normalized: \((x'_{ij}=(x_{ij}-10)/(30-10))\)

Observation X1' X2' X3'
A 0.0 0.5 0.5
B 0.5 0.0 1.0
C 1.0 1.0 0.0

Example Figure

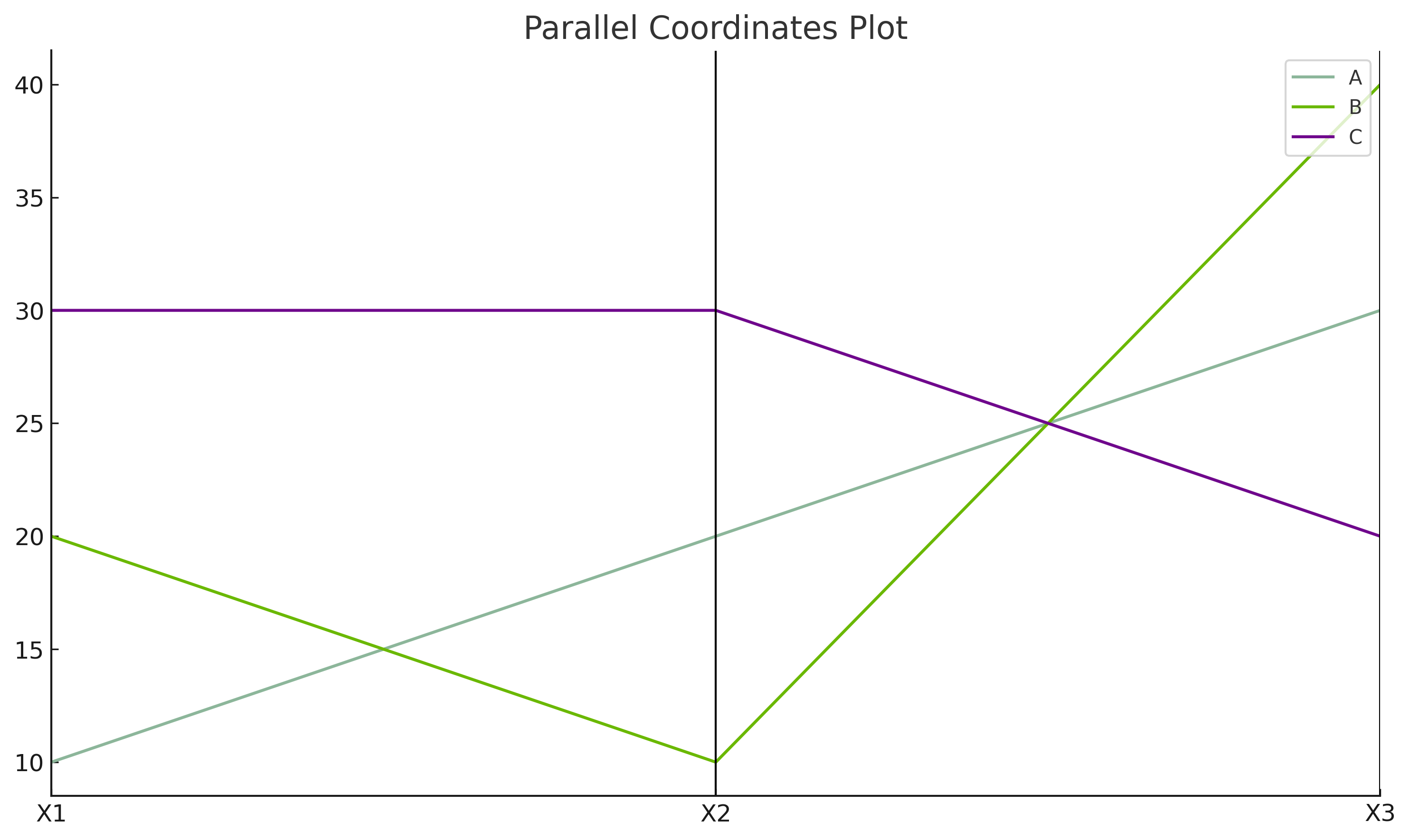
Parallel Coordinates

3️⃣ Deviation Chart

Theory

A Deviation Chart displays differences from a baseline \(( b_j )\) for each variable \(( j )\):
\(( d_{ij} = x_{ij} - b_j )\)

Manual Example

Baseline \((b=[50,30,20])\). Observations:
- A = [55, 25, 20] → \((d_A=[+5,-5,0])\)
- B = [45, 35, 25] → \((d_B=[-5,+5,+5])\)
- C = [60, 40, 15] → \((d_C=[+10,+10,-5])\)

Example Figure

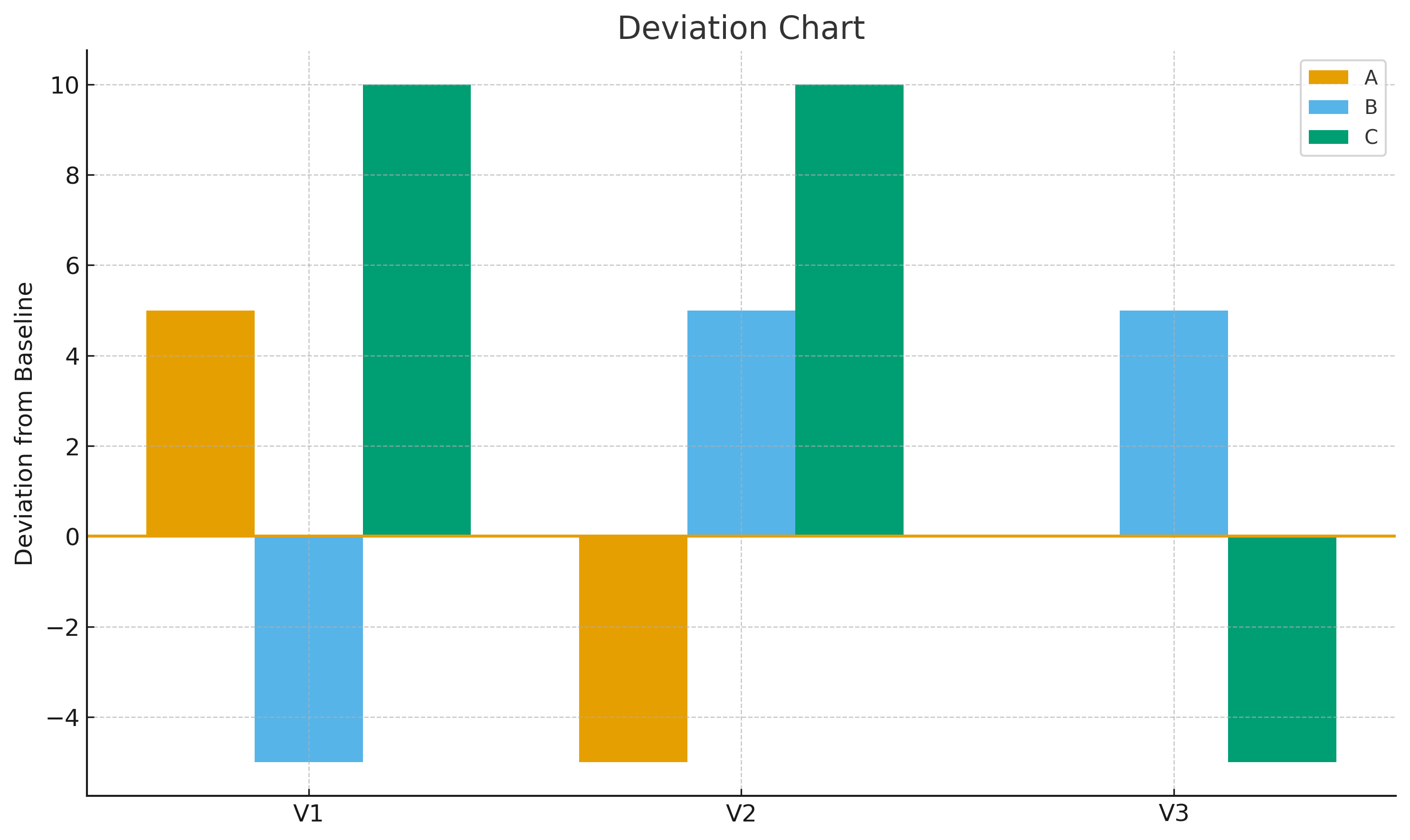
Deviation Chart

4️⃣ Andrews Curves

Theory

Each data point in \((\mathbb{R}^p)\) is represented by

\[ f_i(t) = \frac{x_{i1}}{\sqrt{2}} + x_{i2}\sin(t) + x_{i3}\cos(t) + x_{i4}\sin(2t) + x_{i5}\cos(2t) + \cdots, \]

with \((t\in[-\pi,\pi])\). Curve similarity reflects data similarity.

Manual Example (3 features)

For A(1,2,3) and B(2,1,0): $$ f_A(t) = 1/\sqrt{2} + 2\sin t + 3\cos t,\; f_B(t) = 2/\sqrt{2} + \sin t. $$ Evaluate at \((t=0,\pi/2,\pi)\) to compare values and shapes.

Example Figure

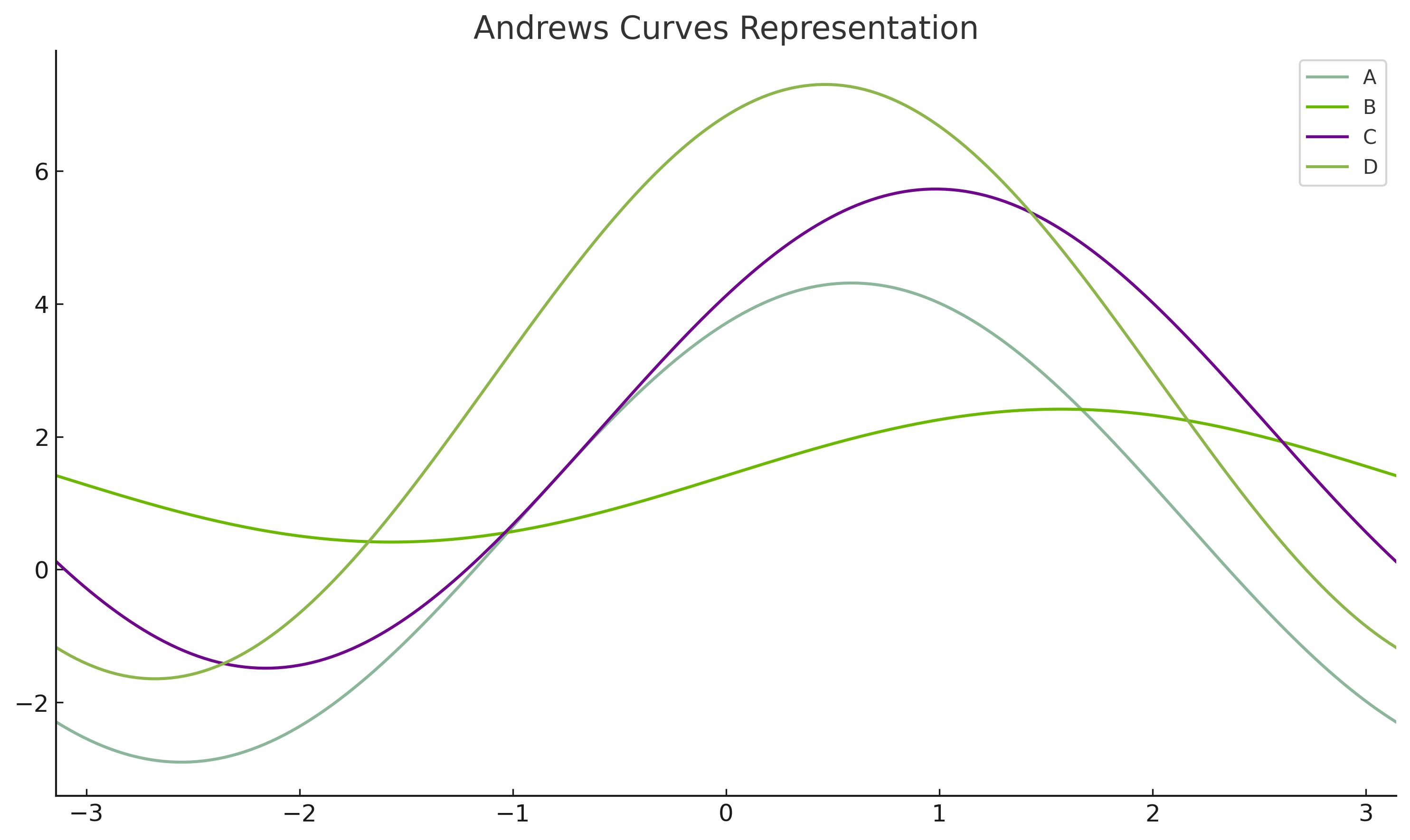
Andrews Curves

5️⃣ Practice Problems (By Hand)

  1. PCP: Normalize and sketch lines for A(1,2,3,4), B(4,3,2,1), C(2,2,2,2). Identify negatively correlated pairs.
  2. Deviation: With baseline [10,20,30], compute deviations for P(12,18,33), Q(9,21,27) and interpret.
  3. Andrews: Compute \((f(t))\) for x=(1,0,2) at \((t=0,\pi/2,\pi)\) and compare with y=(2,1,1).