Skip to content

📘 Chapter 4 — Basic Statistical Descriptions of Data

Measuring central tendency (Mean, Median, Mode) and dispersion (Range, Quartiles, Variance, Standard Deviation, Interquartile Range). Includes worked examples, formulas.

1. Central Tendency

1.1 Mean (Arithmetic Average)

For a sample \(x_1,\dots,x_n\),

\[ \bar{x}=\frac{1}{n}\sum_{i=1}^{n} x_i. \]

1.2 Median (50th Percentile)

Middle value after sorting; for even \(n\), average the two middle values.

1.3 Mode

Most frequent value (or, for continuous data, the modal bin with highest frequency).

Figure: Histogram with mean/median/mode markers
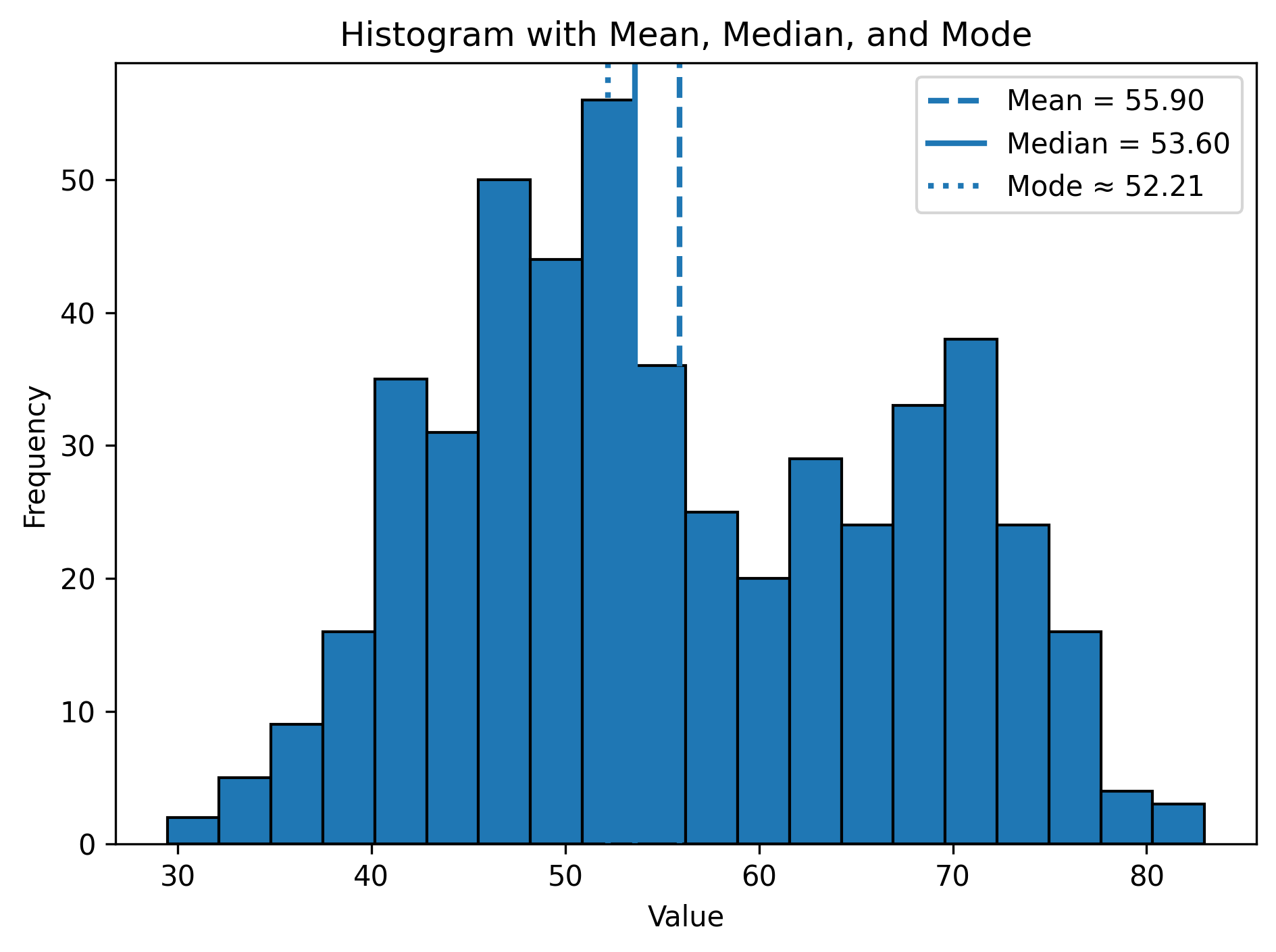
Mean, Median, Mode

2. Dispersion of Data

2.1 Range

\[ \text{Range} = \max(x) - \min(x). \]

2.2 Quartiles & IQR

Quartiles \(Q_1, Q_2, Q_3\) split the ordered data into four parts.
Interquartile Range (IQR):

\[ \text{IQR} = Q_3 - Q_1. \]

Figure: Boxplot with quartiles and whiskers
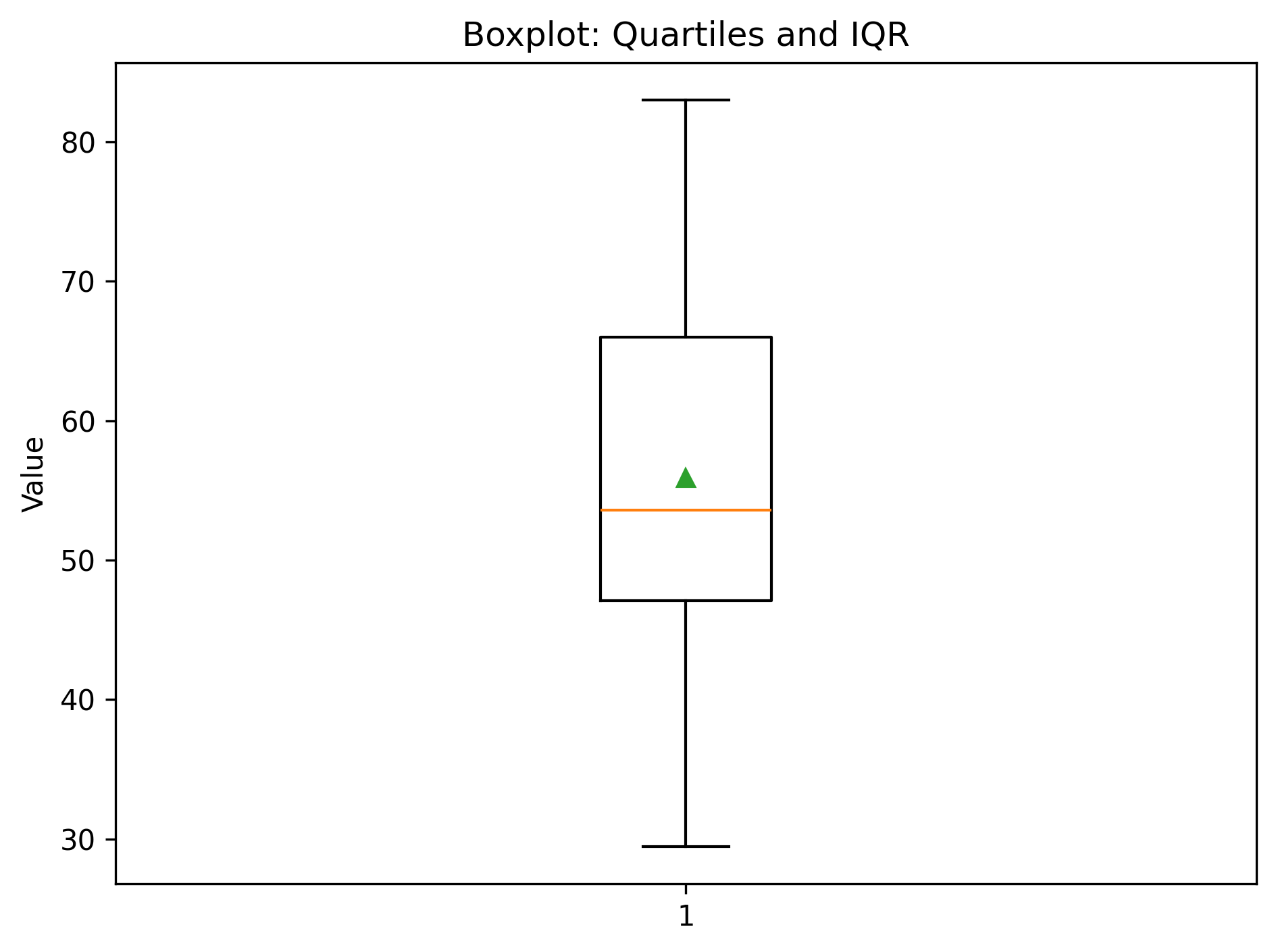
Quartiles & IQR

2.3 Variance & Standard Deviation

Sample variance \(s^2\) and standard deviation \(s\):

\[ s^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2, \qquad s = \sqrt{s^2}. \]

Figure: Deviations from the mean (visualizing variance & std)
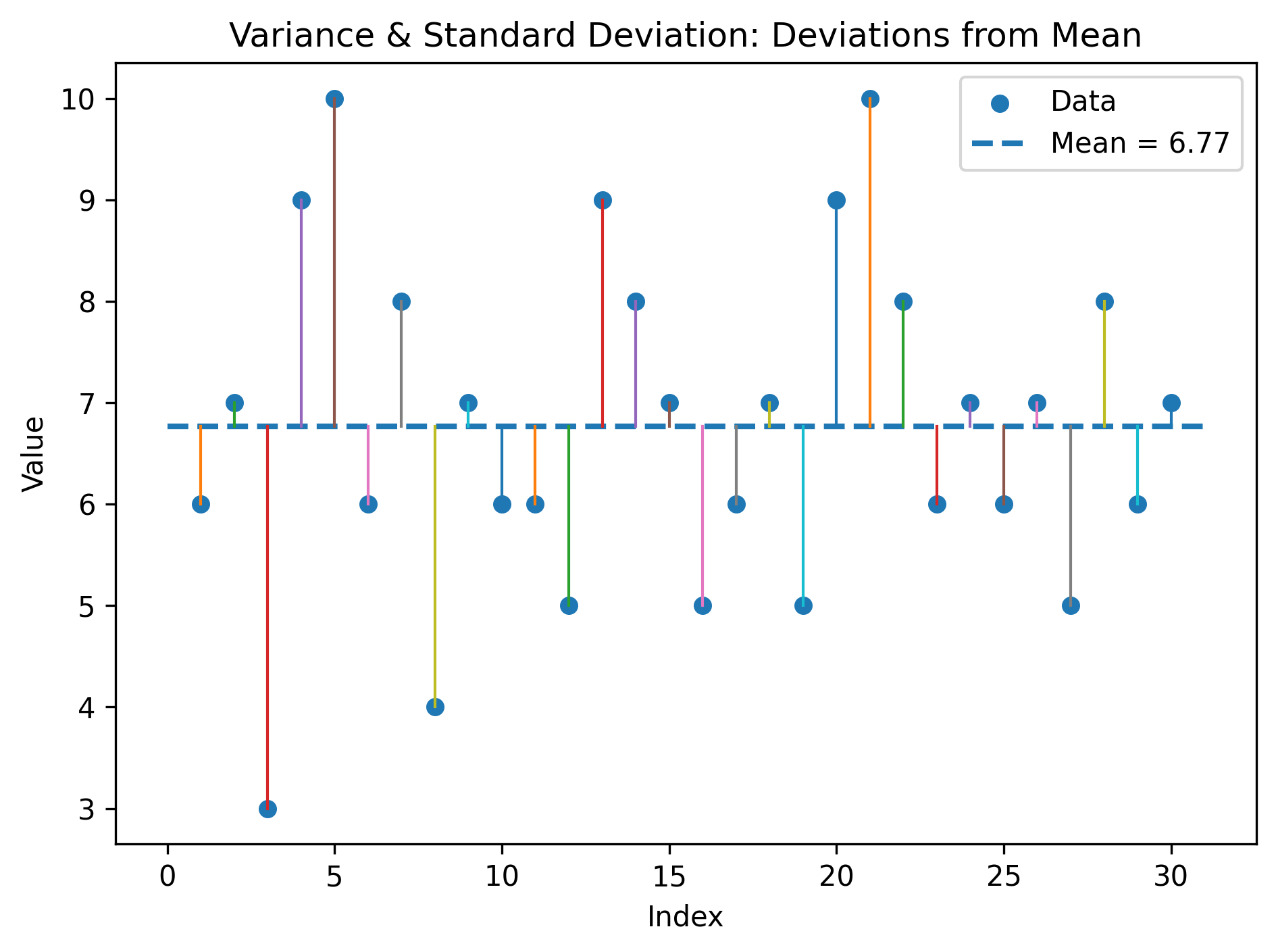
Variance & Standard Deviation

3. Worked Numerical Example (by hand)

Given the sample (n=10):
\(\{6,\, 7,\, 3,\, 9,\, 10,\, 6,\, 8,\, 4,\, 7,\, 6\}\)

  1. Sort: \( \{3,4,6,6,6,7,7,8,9,10\} \)
  2. Mean: \( \bar{x}=\frac{3+4+6+6+6+7+7+8+9+10}{10}=6.6 \)
  3. Median: average of 5th & 6th elements \( \Rightarrow (6+7)/2=6.5 \)
  4. Mode: 6 (most frequent)
  5. Range: \(10-3=7\)
  6. Quartiles (Tukey):
  7. \(Q_1=\) median of lower half \(\{3,4,6,6,6\}=6\)
  8. \(Q_2=\) median \(=6.5\)
  9. \(Q_3=\) median of upper half \(\{7,7,8,9,10\}=8\)
  10. \(\text{IQR}=Q_3-Q_1=2\)
  11. Variance & Std: compute \(\sum (x_i-\bar{x})^2 = 46.4\)
  12. \(s^2 = 46.4/(10-1) \approx 5.156\)
  13. \(s \approx 2.271\)

4. Practice Questions

  1. Prove that the mean minimizes the sum of squared deviations \( \sum (x_i - c)^2 \).
  2. Show, by example, a dataset where mean ≠ median due to skewness.
  3. Compare IQR vs standard deviation as dispersion measures for heavy‑tailed data.
  4. For a bimodal distribution, discuss the usefulness of “mode” and propose alternatives.