🎯 Chapter 17 — Model Evaluation¶

Generalization error, out-of-sample evaluation, overfitting vs underfitting, cross-validation, and metrics for both regression and classification. Includes math, worked examples, Mermaid diagrams.

1) Generalization Error & Out-of-Sample Evaluation¶

Goal: Estimate how well a model will perform on unseen data.

Let data distribution be \(\mathcal{D}\) and loss \(L\). The generalization error of a learned predictor \(\hat f\) is:

\[\mathcal{E}_{\text{gen}}(\hat f) = \mathbb{E}_{(x,y)\sim \mathcal{D}}[L(y, \hat f(x))]. \]

Since \(\mathcal{D}\) is unknown, we estimate with a test set:

\[\hat{\mathcal{E}}_{\text{test}}(\hat f) = \frac{1}{m} \sum_{i=1}^{m} L(y_i, \hat f(x_i)). \]

graph TD
    A[Dataset] --> B[Train Set]
    A --> C[Validation Set]
    A --> D[Test Set]
    B --> E[Train Model]
    C --> F[Tune Hyperparameters]
    D --> G[Final Out-of-Sample Estimate]

2) Bias–Variance Tradeoff (Regression)¶

For squared loss:

\[\mathbb E[(y-\hat f(x))^2] = (\mathbb E[\hat f(x)] - f(x))^2 + \mathbb Var[\hat f(x)] + \sigma^2. \]

Underfitting → high bias, low variance (too simple).
Overfitting → low bias, high variance (too complex).

Visualization:
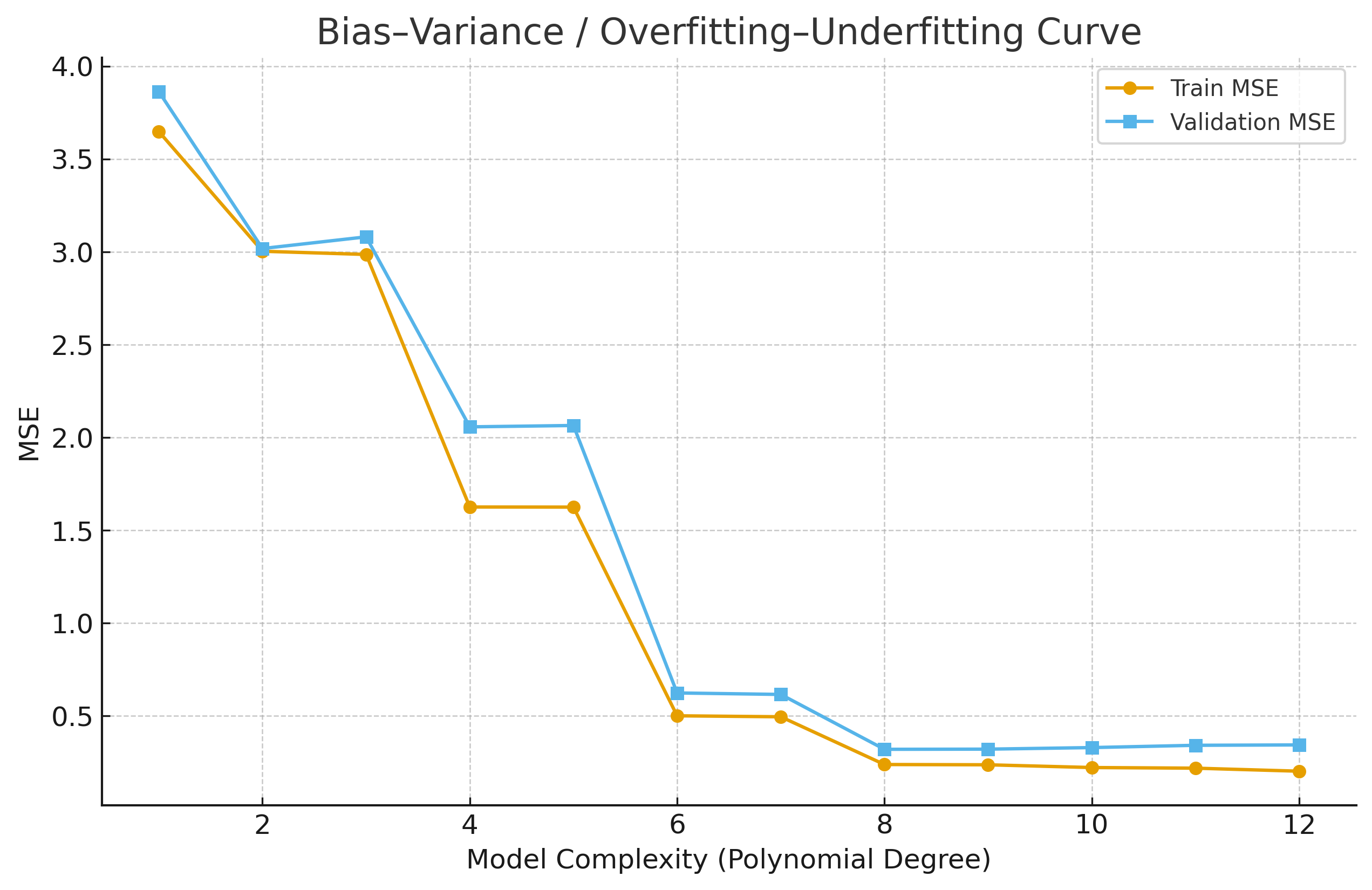
Bias–Variance Curve

3) Evaluation Metrics¶

3.1 Regression Metrics¶

Metric	Formula	Interpretation
MAE	\(\frac{1}{n}\sum_i\\|y_i - \hat y_i\\|\)	Average absolute error
MSE	\(\frac{1}{n}\sum_i (y_i - \hat y_i)^2\)	Penalizes large errors
RMSE	\(\sqrt{\text{MSE}} \)	Root of MSE
R²	\( 1 - \frac{\sum_i (y_i-\hat y_i)^2}{\sum_i (y_i-\bar y)^2}\)	Variance explained

Manual example (tiny):
True: [2, 3, 5, 4, 7], Pred: [2.0, 3.1, 4.2, 5.3, 6.4] → MAE=0.56, MSE=0.54, RMSE≈0.73, R²≈0.82

3.2 Classification Metrics¶

Confusion matrix (binary):

	Predicted +	Predicted -
Actual +	TP	FN
Actual -	FP	TN

Accuracy: \( \frac{TP+TN}{TP+FP+TN+FN} \)
Precision: \( \frac{TP}{TP+FP} \)
Recall (TPR): \( \frac{TP}{TP+FN} \)
F1: \( 2\cdot \frac{PR}{P+R} \)
AUC: area under ROC curve (threshold-independent).

4) Cross-Validation¶

k‑Fold Cross Validation: Divide data into k folds; train on k−1 and validate on the remaining fold.

\[\hat S_{\text{CV}} = \frac{1}{k}\sum_{j=1}^k S(\hat f^{(-j)}, V_j) \]

Stratified CV: keeps class balance (classification).
LOOCV: each fold has one sample; high variance.

Visualization:
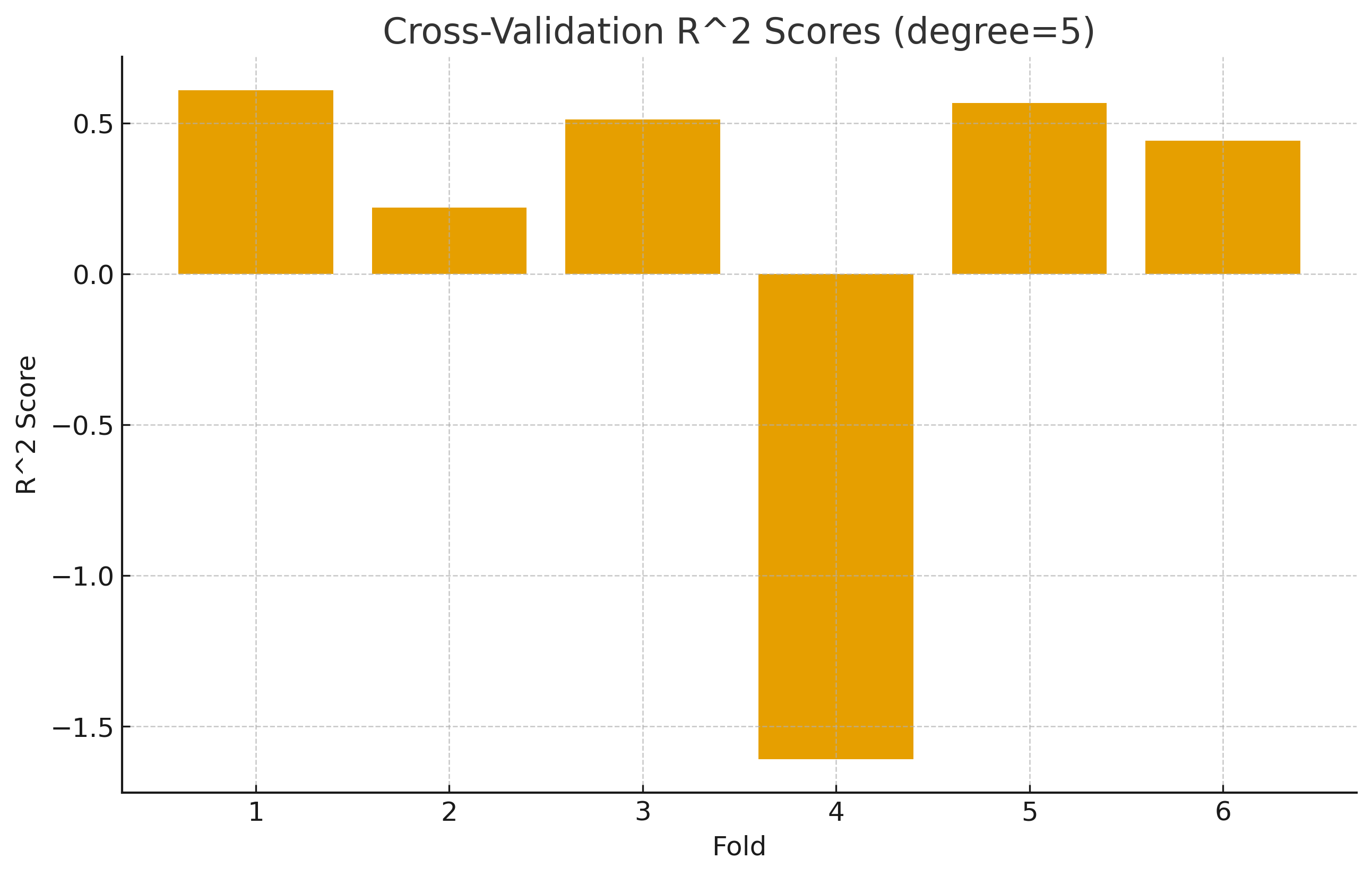
Cross-Validation Scores

5) Overfitting vs Underfitting – Quick Guide¶

Situation	Train Error	Validation Error	Description
Underfitting	High	High	Model too simple
Overfitting	Low	High	Model too complex
Good Fit	Low	Low	Balanced generalization

6) Practice Questions¶

Derive the bias–variance decomposition for squared loss.
Explain why test data must remain untouched until final evaluation.
Demonstrate k-fold CV on small data by hand.
Compute Accuracy, Precision, Recall, and F1 from a confusion matrix.
Explain how cross-validation mitigates overfitting.