🧩 Chapter 16 — Clustering¶

Principles of clustering, k-Means algorithm (math + by-hand example), and evaluation metrics (SSE/Inertia, Silhouette, Davies–Bouldin).

1) Clustering Principles¶

Goal: Group data into clusters so that within-cluster points are similar and between-cluster points are dissimilar.

graph TD
    A[Unlabeled Data] --> B[Clustering Algorithm]
    B --> C[Clusters]

Similarity / Distance¶

Common choice for numeric data is Euclidean distance:

\[ d(\mathbf x_i,\mathbf x_j)=\lVert \mathbf x_i-\mathbf x_j\rVert_2 = \sqrt{ \sum_{p=1}^P (x_{ip}-x_{jp})^2 } . \]

2) k-Means: Objective and Algorithm¶

2.1 Objective¶

Given data $X=\{\mathbf x_i\}_{i=1}^n$, partition into $k$ clusters with centers $ \{\boldsymbol\mu_c\}_{c=1}^k $ by minimizing:

\[ \text{SSE} = \sum_{c=1}^k \ \sum_{\mathbf x_i \in C_c} \lVert \mathbf x_i - \boldsymbol\mu_c \rVert^2. \]

2.2 Alternating Minimization¶

Assignment step: assign each point to nearest center
$ r_{ic} = 1 $ if $ c = \arg\min_j \lVert \mathbf x_i - \boldsymbol\mu_j \rVert $, else $0$.
Update step: update each center to the mean of its assigned points
$ \boldsymbol\mu_c = \frac{1}{|C_c|}\sum_{\mathbf x_i\in C_c}\mathbf x_i $.

Repeat until assignments stop changing or SSE converges.

  flowchart TD
      S[Start: choose k, init centers] --> A[Assign points to nearest center]
      A --> B[Update centers = mean of assigned points]
      B --> C{{Converged?}}
      C -- No --> A
      C -- Yes --> E[Return clusters + centers]

2.3 By‑hand Mini Example (2D, k=2)¶

Points: $ (0,0),(1,0),(0,1), (5,5),(6,5),(5,6) $.
Init centers: $ \mu_1=(0,0), \mu_2=(5,5) $.
- Assign first 3 near $ \mu_1 $, last 3 near $ \mu_2 $.
- Update: $ \mu_1=(\tfrac{1}{3},\tfrac{1}{3}), \mu_2=(\tfrac{16}{3},\tfrac{16}{3}) $.
- Reassign → unchanged ⇒ converged.

3) Evaluation Parameters & Metrics¶

3.1 SSE / Inertia¶

$ \text{SSE} $ is the within-cluster sum of squared distances. Lower is better (for fixed $k$).
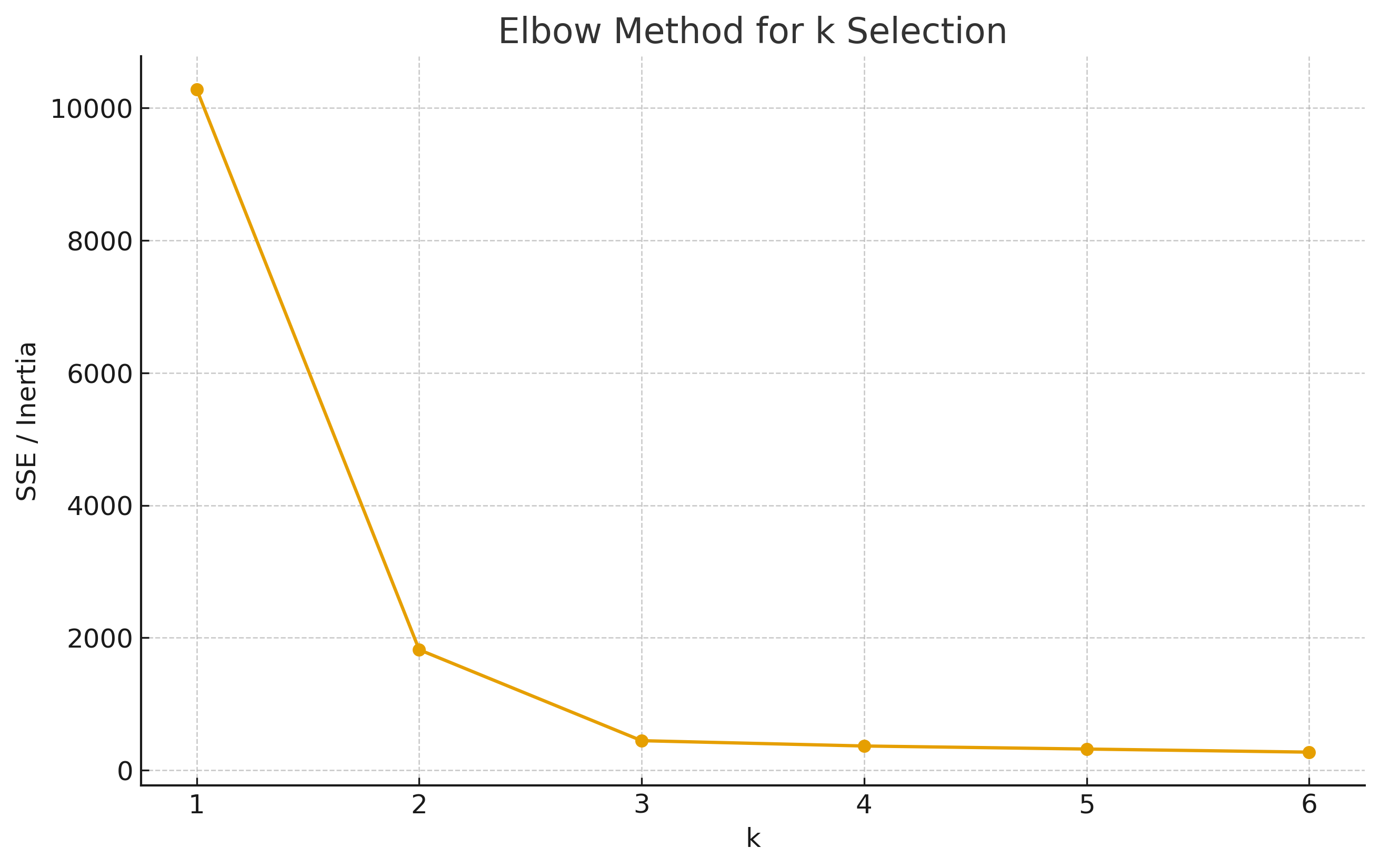
Used by the Elbow method: plot SSE vs $k$ and look for a “knee” where marginal gain drops.

3.2 Silhouette Coefficient¶

For point $i$:
$ a(i) $ = average distance to points in its own cluster;
$ b(i) $ = minimum average distance to other clusters.
Silhouette: $$ s(i)=\frac{b(i)-a(i)}{\max{a(i),\,b(i)}}\in[-1,1]. $$ Overall score is the mean $s(i)$. Higher is better.

3.3 Davies–Bouldin (DB) Index¶

For cluster $c$, let $S_c$ be average distance of points in $c$ to center $\mu_c$; and $M_{cd}=\lVert \mu_c-\mu_d\rVert$.
For each $c$, compute $R_{cd}=\frac{S_c+S_d}{M_{cd}}$ for $d\ne c$, then

$$ \text{DB}=\frac{1}{k}\sum_{c=1}^k \max_{d\ne c} R_{cd}. $$ Lower DB is better (compact & well-separated clusters).

4) Visualizations (Synthetic 2‑D)¶

4.1 k-Means Clusters (k=3)¶

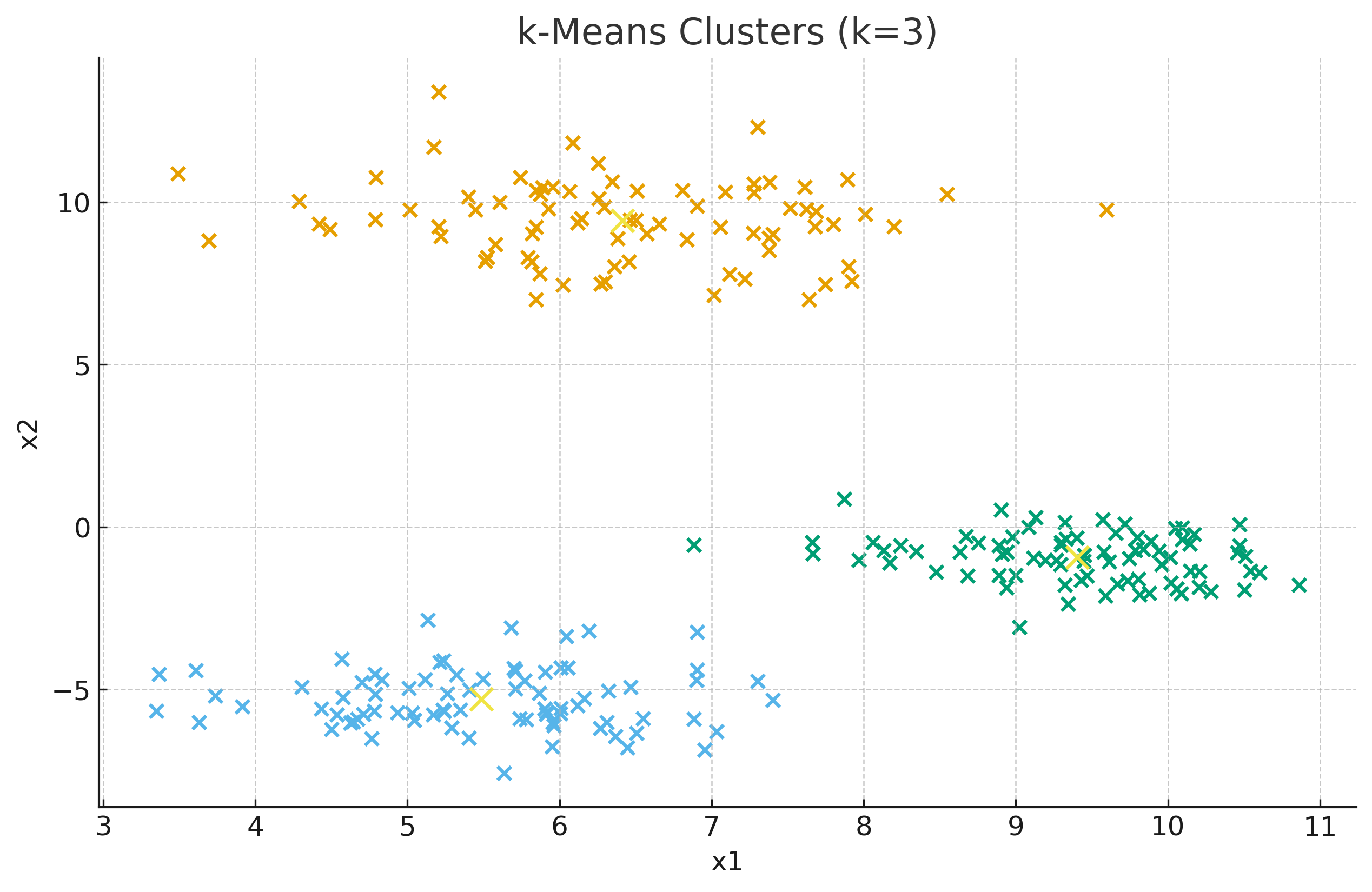
k-Means clusters

4.2 Elbow Method¶

Elbow method

6) Practice Questions¶

Show that the k-Means center update is the mean of assigned points by minimizing SSE.
For the by-hand two‑cluster example, compute SSE after convergence.
Compare the effect of Euclidean vs Manhattan distance for k-Means assignments.
Why can Silhouette be misleading for non‑convex clusters? Suggest an alternative.
Use the Elbow and Silhouette methods together to choose $k$.