Skip to content

🤖 Chapter 15 — Classification

Principles of classification, Confusion Matrix, Precision, Recall, F1, and AUC–ROC with theory, math, a worked example.

1) Classification Principles

Classification predicts discrete labels by learning a function: $$ f: \mathbb{R}^n \to {1,2,\dots,K},\qquad f^* = \arg\min_f\; \mathbb{E}_{(x,y)}[L(y,f(x))]. $$

Binary setup uses a score \(s(x)\) and threshold \(\tau\): $$ \hat y = \begin{cases} 1,& s(x)\ge \tau \ 0,& s(x)<\tau \end{cases} $$

graph TD
    A[Features] --> B[Classifier]
    B --> C[Predicted Label]

2) Confusion Matrix

Predicted + Predicted -
Actual + True Positive (TP) False Negative (FN)
Actual - False Positive (FP) True Negative (TN)

Derived rates: $$ \text{TPR}=\frac{TP}{TP+FN}\quad(\text{Recall}),\qquad \text{FPR}=\frac{FP}{FP+TN}. $$

By‑hand example: TP=8, FP=2, TN=7, FN=3
Accuracy=0.75, Precision=0.80, Recall=0.727, F1≈0.762

Visualization (synthetic):
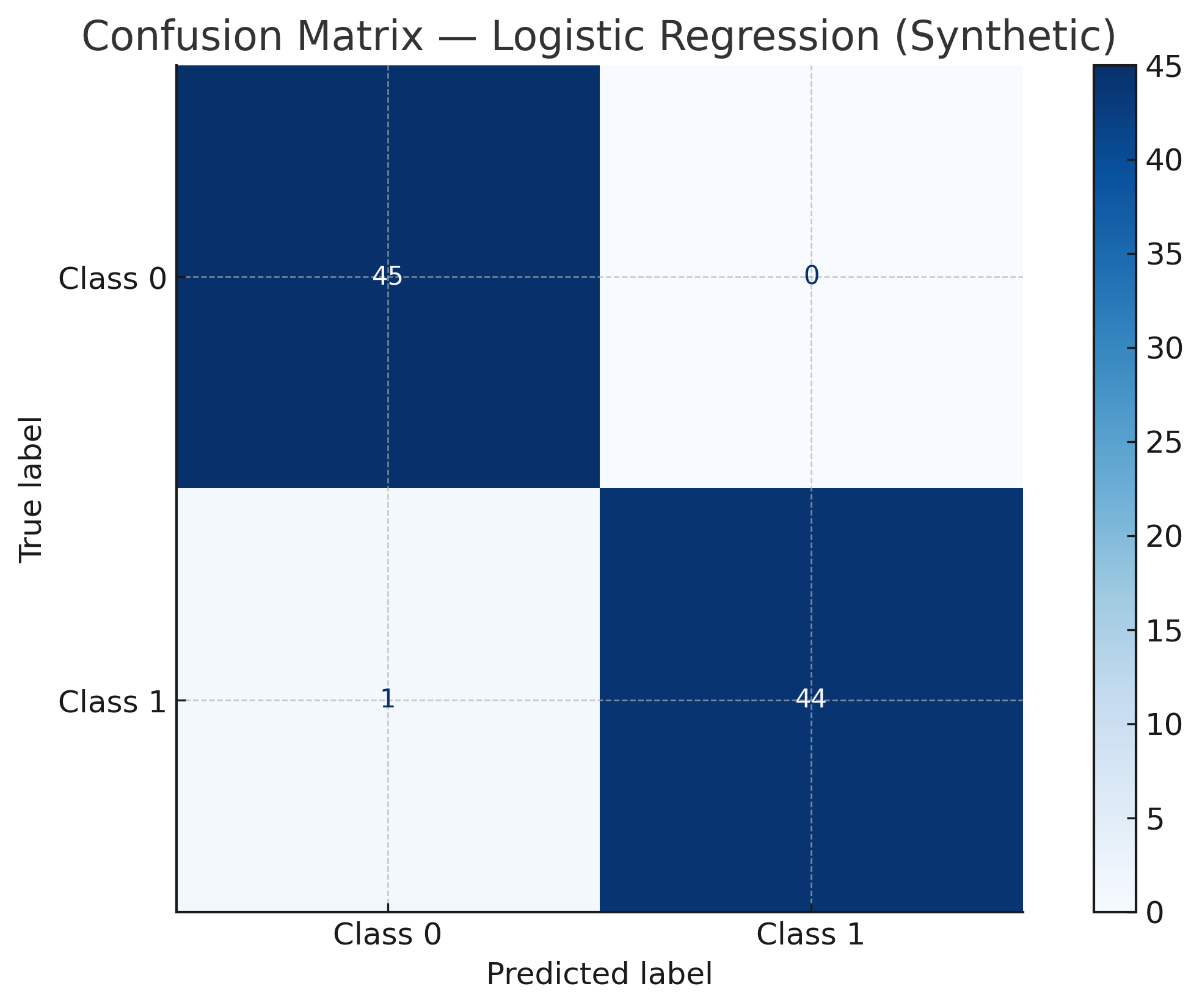
Confusion Matrix

3) Precision, Recall, F1

\[ \text{Precision}=\frac{TP}{TP+FP},\quad \text{Recall}=\frac{TP}{TP+FN},\quad F_1=2\cdot\frac{PR}{P+R}. \]

When to favor each: Precision (costly FP), Recall (costly FN), F1 (balance).

4) ROC Curve and AUC

Vary \(\tau\) to get points \((\text{FPR}(\tau),\text{TPR}(\tau))\) forming the ROC curve.
AUC = area under ROC; probability a random positive is ranked above a random negative.

Visualization (synthetic):
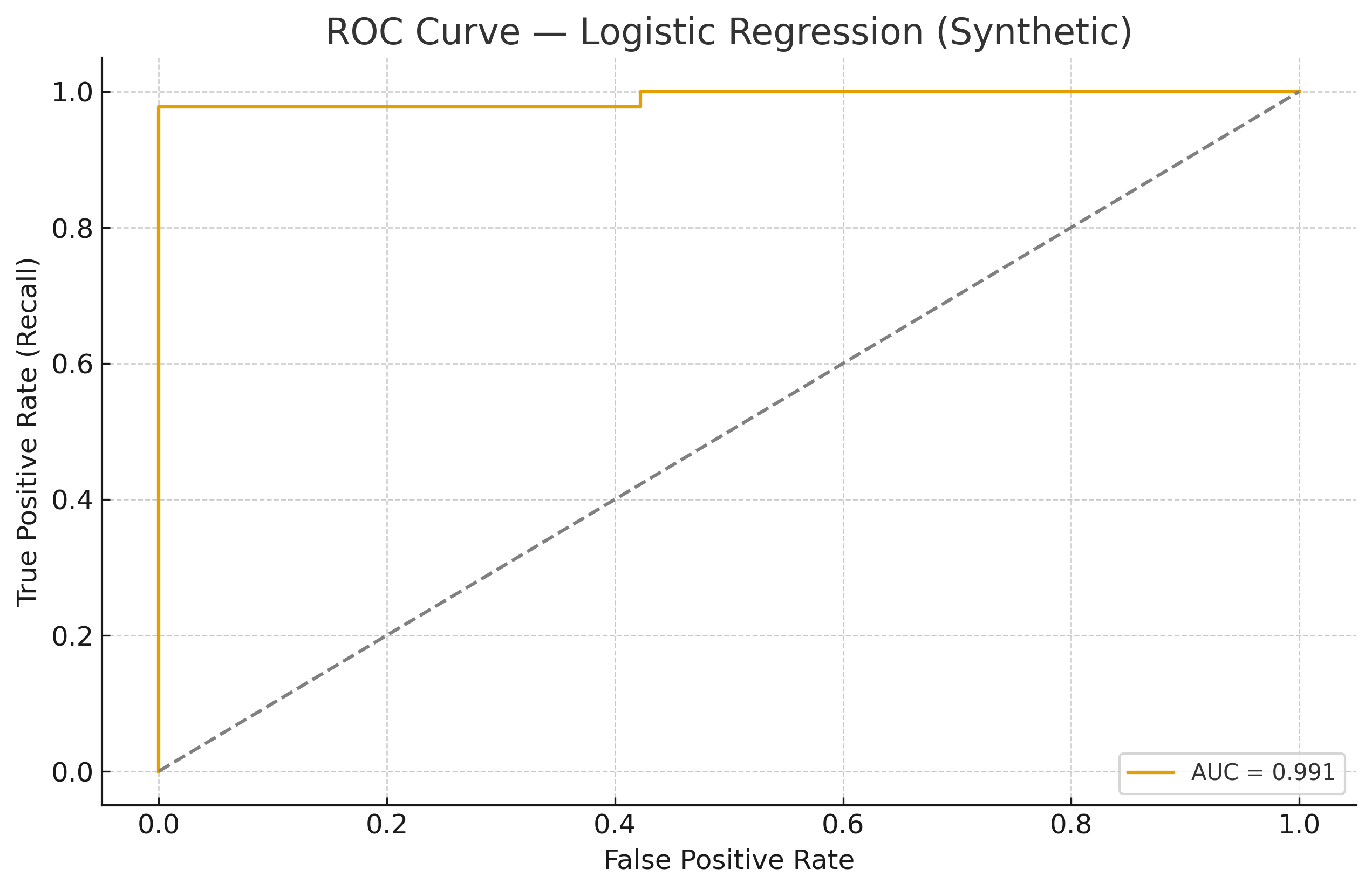
ROC Curve

6) Practice Questions

  1. Derive Precision, Recall, and F1 from the confusion matrix.
  2. Explain why AUC is threshold‑independent.
  3. Compare ROC and Precision–Recall curves.
  4. Why can accuracy be misleading for imbalanced datasets?
  5. Show how moving the decision threshold affects Precision and Recall.